I’ve written a simple league table generator in the style of my fixtures generator.
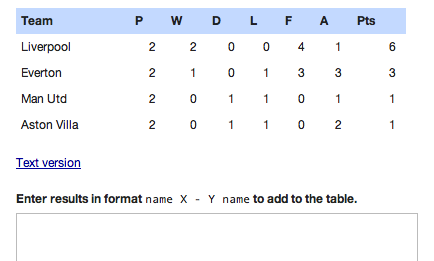
Source code, for those that are interested in such things …
Source code on github
<?php
require_once('masort.php');
function main() {
$s = "";
$cmd = (isset($_REQUEST['cmd']) ? $_REQUEST['cmd'] : null);
$id = (isset($_GET['id']) ? $_GET['id'] : null);
$title = "";
if ($cmd === 'add') {
list($id, $display) = add($id, $_POST['results']);
$s .= $display;
$title = ($id ? "Table $id" : 'Create Table');
}
if ($id) {
if (isset($_GET['txt'])) {
$s .= "<pre>" . table_text($id) . "</pre>";
} else {
$s .= table($id);
}
$title = "Table $id";
}
$s = head($title, $id) . $s;
$s .= input_form($id);
$s .= ($id ? results($id) : "");
$s .= table_links();
$s .= foot();
echo $s;
}
// String of HTML input form for results.
function input_form($id) {
$instructions = '<p class="instructions"><b>Enter results in format</b> <code>name X - Y name</code> <b>to ';
$instructions .= ($id ? "add to the" : "start a new");
$instructions .= " table.</b></p>";
ob_start();
?>
<form method="POST">
<input type="hidden" name="cmd" value="add" />
<input type="hidden" name="id" value="<?php echo h($id); ?>" />
<?php echo $instructions; ?>
<textarea name="results"></textarea>
<p><input type="submit" value="Add" /></p>
</form>
<?php
echo ($id ? "" : "<p>Example: <pre>Liverpool 1 - 0 Man Utd\nEverton 2 - 0 Aston Villa\nLiverpool 3 - 1 Everton\nAston Villa 0 - 0 Man Utd</pre>");
return ob_get_clean();
}
// Add results to a table, creating the table if necessary.
//TODO if we just created a table we won't display it here but we should.
function add($provided_id, $s) {
$id = ($provided_id ? $provided_id : generate_id());
$results = parse_results($s);
$added = 0;
foreach ($results as $r) {
extract($r);
$sql = "INSERT INTO result (table_id, home, away, for, against) VALUES ";
$sql .= "(" . q($id) . ", " . q($home) . ", " . q($away) . ", " . q($for) . ", " . q($against) . ")";
$added += db($sql);
}
if (! $provided_id) {
header("Location: " . self_ref_url() . "?id=" . $id);
return;
}
ob_start();
?>
<p class="success">Added <?php echo $added; ?> results to the table.</p>
<?php
return array($id, ob_get_clean());
}
// String of HTML display of table $id.
function table($id) {
$table = generate_table($id);
$s = "<table><thead><tr><th>Team</th><th>P</th><th>W</th><th>D</th><th>L</th><th>F</th><th>A</th><th>Pts</th></tr></thead><tbody>";
foreach ($table as $team) {
extract(hmap($team));
$s .= "<tr><td>$name</td><td class=\"n\">$played</td><td class=\"n\">$won</td><td class=\"n\">$drawn</td><td class=\"n\">$lost</td><td class=\"n\">$for</td><td class=\"n\">$against</td><td class=\"n\">$points</td></tr>";
}
$s .= "</tbody>";
$s .= '<p><a href="' . self_ref_url() . '?id=' . h($id) . '&txt=1">Text version</a></p>';
return $s;
}
// String of display of table $id suitable for display in monospace font.
function table_text($id) {
$EXTRA_PADDING = 2;
$table = generate_table($id);
list($longest, $numeric) = array(array(), array());
foreach ($table as $team) {
foreach (hmap($team) as $k => $v) {
$longest[$k] = (isset($longest[$k]) && $longest[$k] >= mb_strlen($v) ? $longest[$k] : mb_strlen($v));
$numeric[$k] = (isset($numeric[$k]) ? $numeric[$k] && is_numeric($v) : is_numeric($v));
}
}
$s = "";
foreach ($longest as $k => $max) {
$display = ucwords(strlen($k) > $longest[$k] ? substr($k, 0, 1) : $k);
if ($numeric[$k]) {
$s .= str_pad($display, $max + $EXTRA_PADDING, " ", STR_PAD_LEFT);
} else {
$s .= str_pad($display, $max + $EXTRA_PADDING);
}
}
foreach ($table as $team) {
$s .= "\n";
foreach (hmap($team) as $k => $v) {
if ($numeric[$k]) {
$s .= str_pad($v, $longest[$k] + $EXTRA_PADDING, " ", STR_PAD_LEFT);
} else {
$s .= str_pad($v, $longest[$k] + $EXTRA_PADDING);
}
}
}
$s .= '<p><a href="' . self_ref_url() . '?id=' . h($id) . '">HTML version</a></p>';
return $s . "\n";
}
// String of HTML results.
function results($id) {
$rs = get_results($id);
$s = '<table><tbody>';
foreach ($rs as $r) {
extract(hmap($r));
$s .= "<tr><td>$home</td><td>$for</td><td>-</td><td>$against</td><td>$away</td></tr>";
}
return $s . "</tbody></table>";
}
// String of HTML links to all known tables.
function table_links() {
$sql = "SELECT DISTINCT(table_id) AS id FROM result ORDER BY table_id";
$rs = db($sql);
if (! is_array($rs)) { return ""; }
$s = "";
foreach ($rs as $r) {
extract(hmap($r));
$s .= '<p><a href="?id=' . $id . '">Table ' . $id . '</a></p>';
}
return $s;
}
// ********** Helpers **********
function get_results($id) {
$sql = "SELECT home, away, for, against FROM result WHERE table_id = " . q($id);
return db($sql);
}
function generate_table($id) {
$rs = get_results($id);
$table = array();
foreach ($rs as $r) {
extract($r);
$table = add_result($table, $home, $for, $against);
$table = add_result($table, $away, $against, $for);
}
masort($table, 'points_d,for_d,against_a'); //TODO sort should be more complicated for GD etc.
return $table;
}
function parse_results($s) {
$s = preg_replace('/[ \t]+/', ' ', $s);
$matches = explode("\n", $s);
$results = array();
foreach ($matches as $match) {
if (preg_match('/^(.*?) (\d+) - (\d+) (.*?)$/', $match, $details)) {
$results[] = array('home' => trim($details[1]), 'for' => trim($details[2]), 'against' => trim($details[3]), 'away' => trim($details[4]));
}
}
return $results;
}
function add_result($table, $team, $for, $against) {
if (! isset($table[$team])) {
$table[$team] = array('name' => $team, 'played' => 0, 'won' => 0, 'drawn' => 0, 'lost' => 0, 'for' => 0, 'against' => 0, 'points' => 0);
}
if ($for > $against) {
$table[$team]['won'] += 1;
$table[$team]['points'] += 3;
} else if ($for < $against) {
$table[$team]['lost'] += 1;
} else {
$table[$team]['drawn'] += 1;
$table[$team]['points'] += 1;
}
$table[$team]['played'] += 1;
$table[$team]['for'] += $for;
$table[$team]['against'] += $against;
return $table;
}
// Get next table id in the database. Unsafe.
function generate_id() {
$sql = "SELECT IFNULL(MAX(table_id), 0) + 1 AS result FROM result";
$rs = db($sql);
return $rs[0]['result'];
}
// ********* Header/Footer **********
// String of HTML header.
function head($title, $id) {
ob_start();
?>
< !DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01//EN" "http://www.w3.org/TR/html4/strict.dtd">
<html>
<head>
<title>League Table Generator<?php if ($title) { echo " - $title"; } ?></title>
<link rel="stylesheet" href="blueprint/screen.css" type="text/css" media="screen, projection">
</link><link rel="stylesheet" href="blueprint/print.css" type="text/css" media="print">
<!--[if lt IE 8]>
</link><link rel="stylesheet" href="css/blueprint/ie.css" type="text/css" media="screen, projection">
< ![endif]-->
<link rel="stylesheet" type="text/css" href="table.css" />
</link></head>
<body>
<div class="container">
<div class="span-10 last">
<h1>Table Generator</h1>
<p>This program is part of <a href="/2009/09/league-table-generator">bluebones.net</a></p>
<?php if ($title) { echo "<h2>$title"; } ?>
<?php if ($id) { ?>
<p><a href="<?php echo h($_SERVER['SCRIPT_NAME']); ?>">New Table</a></p>
<?php } ?>
<?php
return ob_get_clean();
}
// String of HTML footer.
function foot() {
ob_start();
?>
</div>
</div>
</body>
</html>
<?php
return ob_get_clean();
}
// ********** Utilities **********
function self_ref_url() {
$host = $_SERVER['HTTP_HOST'];
$uri = $_SERVER['PHP_SELF'];
return "http://$host$uri";
}
// SQL-quote a string.
function q($s) {
return "'" . str_replace("'", "''", $s) . "'";
}
// HTML escaping to prevent XSS
function h($s) {
return htmlentities($s);
}
// HTML escape the values of an assoc array
function hmap($a) {
$new = array();
foreach ($a as $k => $v) {
$new[$k] = h($v);
}
return $new;
}
// Exec query on db $id creating it if necessary and returning array of results if a SELECT.
function db($sql) {
$db = sqlite_open('results');
// Create table if it doesn't exist. Ignore error if it does.
@sqlite_exec($db, 'CREATE TABLE result (home VARCHAR(255), away VARCHAR(255), for INT, against INT, table_id INT)');
if (strpos($sql, "SELECT") === 0) {
$q = sqlite_query($db, $sql);
return sqlite_fetch_all($q, SQLITE_ASSOC);
} else {
return sqlite_exec($db, $sql);
}
}
main();
/*
Copyright (c) 2009 Thomas David Baker
Permission is hereby granted, free of charge, to any person
obtaining a copy of this software and associated documentation
files (the "Software"), to deal in the Software without
restriction, including without limitation the rights to use,
copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following
conditions:
The above copyright notice and this permission notice shall be
included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND,
EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES
OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND
NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT
HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY,
WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR
OTHER DEALINGS IN THE SOFTWARE.
*/

